1. 位运算

整数在计算机中用二进制的位来表示，C 语言提供一些运算符可以直接操作整数中的位，称为位运算，这些运算符的操作数都必须是整型的。在以后的学习中你会发现，有些信息利用整数中的某几个位来存储，要访问这些位，仅仅有对整数的操作是不够的，必须借助位运算，例如第 2 节“Unicode 和 UTF-8”介绍的 UTF-8 编码就是如此，学完本节之后你应该能自己写出 UTF-8 的编码和解码程序。本节首先介绍各种位运算符，然后介绍与位运算有关的编程技巧。

1.1. 按位与、或、异或、取反运算

在第 3 节“布尔代数”讲过逻辑与、或、非运算，并列出了真值表，对于整数中的位也可以做与、或、非运算，C 语言提供了按位与（Bitwise AND）运算符&、按位或（Bitwise OR）运算符 | 和按位取反（Bitwise NOT）运算符~，此外还有按位异或（Bitwise XOR）运算符^，我们在第 1 节“为什么计算机用二进制计数”讲过异或运算。下面用二进制的形式举几个例子。

图 16.1. 位运算

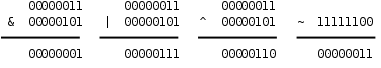
注意，&、|、^ 运算符都是要做 Usual Arithmetic Conversion 的（其中有一步是 Integer Promotion），~ 运算符也要做 Integer Promotion，所以在 C 语言中其实并不存在 8 位整数的位运算，操作数在做位运算之前都至少被提升为int型了，上面用 8 位整数举例只是为了书写方便。比如：

unsigned char c = 0xfc;
unsigned int i = ~c;

计算过程是这样的：常量 0xfc 是int型的，赋给c要转成unsigned char，值不变；c的十六进制表示是 fc，计算~c时先提升为整型（000000fc）然后取反，最后结果是 ffffff03。注意，如果把~c看成是 8 位整数的取反，最后结果就得 3 了，这就错了。为了避免出错，一是尽量避免不同类型之间的赋值，二是每一步计算都要按上一章讲的类型转换规则仔细检查。

1.2. 移位运算

移位运算符（Bitwise Shift）包括左移 << 和右移 >>。左移将一个整数的各二进制位全部左移若干位，例如 0xcfffffff3<<2 得到 0x3fffffcc：

图 16.2. 左移运算

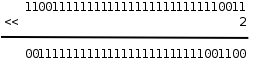
最高两位的 11 被移出去了，最低两位又补了两个 0，其它位依次左移两位。但要注意，移动的位数必须小于左操作数的总位数，比如上面的例子，左边是unsigned int型，如果左移的位数大于等于 32 位，则结果是 Undefined。移位运算符不同于 + - * / == 等运算符，两边操作数的类型不要求一致，但两边操作数都要做 Integer Promotion，整个表达式的类型和左操作数提升后的类型相同。

复习一下第 2 节“不同进制之间的换算”讲过的知识可以得出结论，在一定的取值范围内，将一个整数左移 1 位相当于乘以 2。比如二进制 11（十进制 3）左移一位变成 110，就是 6，再左移一位变成 1100，就是 12。读者可以自己验证这条规律对有符号数和无符号数都成立，对负数也成立。当然，如果左移改变了最高位（符号位），那么结果肯定不是乘以 2 了，所以我加了个前提“在一定的取值范围内”。由于计算机做移位比做乘法快得多，编译器可以利用这一点做优化，比如看到源代码中有i * 8，可以编译成移位指令而不是乘法指令。

当操作数是无符号数时，右移运算的规则和左移类似，例如 0xcfffffff3>>2 得到 0x33fffffc：

图 16.3. 右移运算

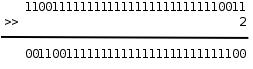
最低两位的 11 被移出去了，最高两位又补了两个 0，其它位依次右移两位。和左移类似，移动的位数也必须小于左操作数的总位数，否则结果是 Undefined。在一定的取值范围内，将一个整数右移 1 位相当于除以 2，小数部分截掉。

当操作数是有符号数时，右移运算的规则比较复杂：

• 如果是正数，那么高位移入 0
• 如果是负数，那么高位移入 1 还是 0 不一定，这是 Implementation-defined 的。对于 x86 平台的gcc编译器，最高位移入 1，也就是仍保持负数的符号位，这种处理方式对负数仍然保持了“右移 1 位相当于除以 2”的性质。

综上所述，由于类型转换和移位等问题，用有符号数做位运算是很不方便的，所以，建议只对无符号数做位运算，以减少出错的可能。

习题

1. 下面两行printf打印的结果有何不同？请读者比较分析一下。%x转换说明的含义详见第 2.9 节“格式化 I/O 函数”。

   int i = 0xcffffff3;
   printf("%x\n", 0xcffffff3>>2);
   printf("%x\n", i>>2);

1.3. 掩码

如果要对一个整数中的某些位进行操作，怎样表示这些位在整数中的位置呢？可以用掩码（Mask）来表示。比如掩码 0x0000ff00 表示对一个 32 位整数的 8~15 位进行操作，举例如下。

1. 取出 8~15 位。

   unsigned int a, b, mask = 0x0000ff00;
   a = 0x12345678;
   b = (a & mask) >> 8; /* 0x00000056 */

   这样也可以达到同样的效果：

   b = (a >> 8) & ~(~0U << 8);

2. 将 8~15 位清 0。

   unsigned int a, b, mask = 0x0000ff00;
   a = 0x12345678;
   b = a & ~mask; /* 0x12340078 */

3. 将 8~15 位置 1。

   unsigned int a, b, mask = 0x0000ff00;
   a = 0x12345678;
   b = a | mask; /* 0x1234ff78 */

习题

1. 统计一个无符号整数的二进制表示中 1 的个数，函数原型是int countbit(unsigned int x);。

2. 用位操作实现无符号整数的乘法运算，函数原型是unsigned int multiply(unsigned int x, unsigned int y);。例如：(11011)₂×(10010)₂=((11011)₂<<1)+((11011)₂<<4)。

3. 对一个 32 位无符号整数做循环右移，函数原型是unsigned int rotate_right(unsigned int x);。所谓循环右移就是把低位移出去的部分再补到高位上去，例如rotate_right(0xdeadbeef, 16)的值应该是 0xefdeadbe。

1.4. 异或运算的一些特性

1. 一个数和自己做异或的结果是 0。如果需要一个常数 0，x86 平台的编译器可能会生成这样的指令：xorl %eax, %eax。不管eax寄存器里的值原来是多少，做异或运算都能得到 0，这条指令比同样效果的movl $0, %eax指令快，因为前者只需要在 CPU 内部计算，而后者需要访问内存，在下一章第 5 节“Memory Hierarchy”详细介绍。

2. 从异或的真值表可以看出，不管是 0 还是 1，和 0 做异或保持原值不变，和 1 做异或得到原值的相反值。可以利用这个特性配合掩码实现某些位的翻转，例如：

   unsigned int a, b, mask = 1U << 6;
   a = 0x12345678;
   b = a ^ mask; /* flip the 6th bit */

3. 如果 a₁ ^ a₂ ^ a₃ ^ ... ^ a_n的结果是 1，则表示 a₁、a₂、a₃...a_n之中 1 的个数为奇数个，否则为偶数个。这条性质可用于奇偶校验（Parity Check），比如在串口通信过程中，每个字节的数据都计算一个校验位，数据和校验位一起发送出去，这样接收方可以根据校验位粗略地判断接收到的数据是否有误。

4. x ^ x ^ y == y，因为 x ^ x == 0，0 ^ y == y。这个性质有什么用呢？我们来看这样一个问题：交换两个变量的值，不得借助额外的存储空间，所以就不能采用temp = a; a = b; b = temp;的办法了。利用位运算可以这样做交换：

   a = a ^ b;
   b = b ^ a;
   a = a ^ b;

分析一下这个过程。为了避免混淆，把 a 和 b 的初值分别记为 a₀和 b₀。第一行，a = a<sub>0</sub> ^ b<sub>0</sub>；第二行，把 a 的新值代入，得到b = b<sub>0</sub> ^ a<sub>0</sub> ^ b<sub>0</sub>，等号右边的 b₀相当于上面公式中的 x，a₀相当于 y，所以结果为 a₀；第三行，把 a 和 b 的新值代入，得到a = a<sub>0</sub> ^ b<sub>0</sub> ^ a<sub>0</sub>，结果为 b₀。注意这个过程不能把同一个变量自己跟自己交换，而利用中间变量temp则可以交换。

习题

1. 请在网上查找有关 RAID（Redundant Array of Independent Disks，独立磁盘冗余阵列）的资料，理解其实现原理，其实就是利用了本节的性质 3 和 4。

2. 交换两个变量的值，不得借助额外的存储空间，除了本节讲的方法之外你还能想出什么方法？本节讲的方法不能把同一个变量自己跟自己交换，你的方法有没有什么局限性？