5. 环形队列
比较 例 12.3“用深度优先搜索解迷宫问题” 的栈操作和 例 12.4“用广度优先搜索解迷宫问题” 的队列操作可以发现,栈操作的 top 指针在 Push 时增大而在 Pop 时减小,栈空间是可以重复利用的,而队列的 head 、 tail 指针都在一直增大,虽然前面的元素已经出队了,但它所占的存储空间却不能重复利用。在 例 12.4“用广度优先搜索解迷宫问题” 的解法中,出队的元素仍然有用,保存着走过的路径和每个点的前趋,但大多数程序并不是这样使用队列的,一般情况下出队的元素就不再有保存价值了,这些元素的存储空间应该回收利用,由此想到把队列改造成环形队列(Circular Queue):把 queue 数组想像成一个圈, head 和 tail 指针仍然是一直增大的,当指到数组末尾时就自动回到数组开头,就像两个人围着操场赛跑,沿着它们跑的方向看,从 head 到 tail 之间是队列的有效元素,从 tail 到 head 之间是空的存储位置,如果 head 追上 tail 就表示队列空了,如果 tail 追上 head 就表示队列的存储空间满了。如下图所示:
图 12.5. 环形队列
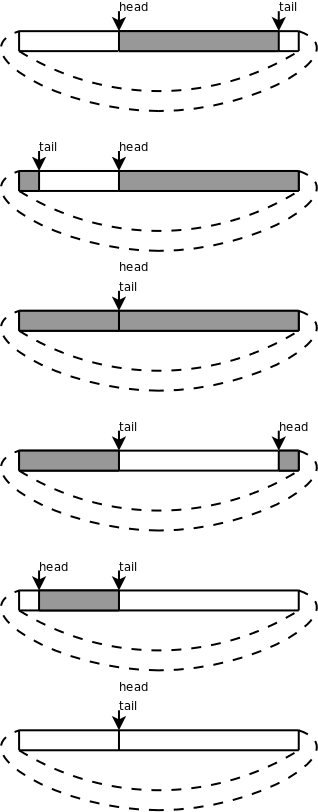
习题
- 现在把迷宫问题的要求改一下,只要求程序给出最后结论就可以了,回答“有路能到达终点”或者“没有路能到达终点”,而不需要把路径打印出来。请把 例 12.4“用广度优先搜索解迷宫问题” 改用环形队列实现,然后试验一下解决这个问题至少需要分配多少个元素的队列空间。