3. 算法的时间复杂度分析
解决同一个问题可以有很多种算法,比较评价算法的好坏,一个重要的标准就是算法的时间复杂度。现在研究一下插入排序算法的执行时间,按照习惯,输入长度 LEN 以下用 n 表示。设循环中各条语句的执行时间分别是 c1、c2、c3、c4、c5 这样五个常数 [1]:
void insertion_sort(void) 执行时间
{
int i, j, key;
for (j = 1; j < LEN; j++) {
key = a[j]; c1
i = j - 1; c2
while (i >= 0 && a[i] > key) {
a[i+1] = a[i]; c3
i--; c4
}
a[i+1] = key; c5
}
}显然外层 for 循环的执行次数是 n-1 次,假设内层的 while 循环执行 m 次,则总的执行时间粗略估计是 (n-1)*(c1+c2+c5+m*(c3+c4))。当然, for 和 while 后面 () 括号中的赋值和条件判断的执行也需要时间,而我没有设一个常数来表示,这不影响我们的粗略估计。
这里有一个问题,m 不是个常数,也不取决于输入长度 n,而是取决于具体的输入数据。在最好情况下,数组 a 的原始数据已经排好序了, while 循环一次也不执行,总的执行时间是 (c1+c2+c5)*n-(c1+c2+c5),可以表示成 an+b 的形式,是 n 的线性函数(Linear Function)。那么在最坏情况(Worst Case)下又如何呢?所谓最坏情况是指数组 a 的原始数据正好是从大到小排好序的,请读者想一想为什么这是最坏情况,然后把上式中的 m 替换掉算一下执行时间是多少。
数组 a 的原始数据属于最好和最坏情况的都比较少见,如果原始数据是随机的,可称为平均情况(Average Case)。如果原始数据是随机的,那么每次循环将已排序的子序列 a[1..j-1]与新插入的元素 key 相比较,子序列中平均都有一半的元素比 key 大而另一半比 key 小,请读者把上式中的 m 替换掉算一下执行时间是多少。最后的结论应该是:在最坏情况和平均情况下,总的执行时间都可以表示成 an2+bn+c 的形式,是 n 的二次函数(Quadratic Function)。
在分析算法的时间复杂度时,我们更关心最坏情况而不是最好情况,理由如下:
- 最坏情况给出了算法执行时间的上界,我们可以确信,无论给什么输入,算法的执行时间都不会超过这个上界,这样为比较和分析提供了便利。
- 对于某些算法,最坏情况是最常发生的情况,例如在数据库中查找某个信息的算法,最坏情况就是数据库中根本不存在该信息,都找遍了也没有,而某些应用场合经常要查找一个信息在数据库中存在不存在。
- 虽然最坏情况是一种悲观估计,但是对于很多问题,平均情况和最坏情况的时间复杂度差不多,比如插入排序这个例子,平均情况和最坏情况的时间复杂度都是输入长度 n 的二次函数。
比较两个多项式 a1n+b1和 a2n2+b2n+c2的值(n 取正整数)可以得出结论:n 的最高次指数是最主要的决定因素,常数项、低次幂项和系数都是次要的。比如 100n+1 和 n2+1,虽然后者的系数小,当 n 较小时前者的值较大,但是当 n>100 时,后者的值就远远大于前者了。如果同一个问题可以用两种算法解决,其中一种算法的时间复杂度为线性函数,另一种算法的时间复杂度为二次函数,当问题的输入长度 n 足够大时,前者明显优于后者。因此我们可以用一种更粗略的方式表示算法的时间复杂度,把系数和低次幂项都省去,线性函数记作 Θ(n),二次函数记作 Θ(n2)。
Θ(g(n)) 表示和 g(n) 同一量级的一类函数,例如所有的二次函数 f(n) 都和 g(n)=n2属于同一量级,都可以用 Θ(n2) 来表示,甚至有些不是二次函数的也和 n2属于同一量级,例如 2n2+3lgn。“同一量级”这个概念可以用下图来说明(该图出自 算法导论):
图 11.2. Θ-notation
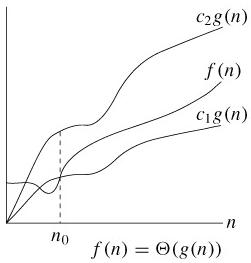
如果可以找到两个正的常数 c1和 c2,使得 n 足够大的时候(也就是 n≥n0的时候)f(n) 总是夹在 c1g(n) 和 c2g(n) 之间,就说 f(n) 和 g(n) 是同一量级的,f(n) 就可以用 Θ(g(n)) 来表示。
以二次函数为例,比如 1/2n2-3n,要证明它是属于 Θ(n2) 这个集合的,我们必须确定 c1、c2和 n0,这些常数不随 n 改变,并且当 n≥n0以后,c1n2≤1/2n2-3n≤c2n2总是成立的。为此我们从不等式的每一边都除以 n2,得到 c1≤1/2-3/n≤c2。见下图:
图 11.3. 1/2-3/n
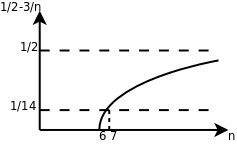
这样就很容易看出来,无论 n 取多少,该函数一定小于 1/2,因此 c2=1/2,当 n=6 时函数值为 0,n>6 时该函数都大于 0,可以取 n0=7,c1=1/14,这样当 n≥n0时都有 1/2-3/n≥c1。通过这个证明过程可以得出结论,当 n 足够大时任何 an2+bn+c 都夹在 c1n2和 c2n2之间,相对于 n2项来说 bn+c 的影响可以忽略,a 可以通过选取合适的 c1、c2来补偿。
几种常见的时间复杂度函数按数量级从小到大的顺序依次是:Θ(lgn),Θ(sqrt(n)),Θ(n),Θ(nlgn),Θ(n2),Θ(n3),Θ(2n),Θ(n!)。其中,lgn 通常表示以 10 为底 n 的对数,但是对于 Θ-notation 来说,Θ(lgn) 和 Θ(log2n) 并无区别(想一想这是为什么),在算法分析中 lgn 通常表示以 2 为底 n 的对数。可是什么算法的时间复杂度里会出现 lgn 呢?回顾插入排序的时间复杂度分析,无非是循环体的执行时间乘以循环次数,只有加和乘运算,怎么会出来 lg 呢?下一节归并排序的时间复杂度里面就有 lg,请读者留心 lg 运算是从哪出来的。
除了 Θ-notation 之外,表示算法的时间复杂度常用的还有一种 Big-O notation。我们知道插入排序在最坏情况和平均情况下时间复杂度是 Θ(n2),在最好情况下是 Θ(n),数量级比 Θ(n2) 要小,那么总结起来在各种情况下插入排序的时间复杂度是 O(n2)。Θ 的含义和“等于”类似,而大 O 的含义和“小于等于”类似。
受内存管理机制的影响,指令的执行时间不一定是常数,但执行时间的上界(Upper Bound)肯定是常数,我们这里假设语句的执行时间是常数只是一个粗略估计。 ↩︎